“It followed from the special theory of relativity that mass and energy are both but different manifestations of the same thing — a somewhat unfamiliar conception for the average mind.” -Albert Einstein
On the one hand, we have matter -- things with mass -- in the Universe, ranging all the way from planets, stars and galaxies on the largest scales to molecules, atoms and fundamental particles on the smallest.
But then, on the other hand, there are particles without mass at all: photons, for example. They still carry energy and momentum, but of all the possibilities, of all the ways that mass and energy could have been related, why is it that the relationship is E = mc^2, without any other constants or factors in there?
As it turns out, a thought experiment can explain it to us. Come find out on this week's Ask Ethan!
- Log in to post comments




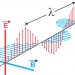


If the box went from zero to finite kinetic energy, does that mean the photon lost some energy - i.e. got redshifted?
The VERY last paragraph resolved a huge misunderstanding on my part all this time!
This whole time, I only ever thought of that formula as a "conversion formula". Put in E energy, and get out MC^2 mass. This left me utterly confused as to exactly WHAT units were being used. What is a single unit of "E" and what is a unit of "M"? (The speed of light was the only obvious part.) I thought "Okay, but what if I use the wrong scale, like I see "E" as a single photon, and "M" as a metric ton? What units do I plug in here?!".
At long last, I get it now. It's not JUST a conversion algorithm! It's a value assignment! It's saying THIS value of "E" has exactly THIS "hidden" value of "M", "inherit" to it, so that WHEN it gets converted, THIS is the amount of "E" that you get. I'm still just a tad confused as to the exact amounts involved (how many kilograms is it worth), but I've got a much better understanding now.
@Dark Jaguar #2: You're exactly right to do the dimensional analysis! If you use SI ("metric") units, then everything works out without any special factors. Energy is measured in joules (kg-m^2/s^2), mass in kilograms and speed in m/s.
The speed of light in vacuum (c), exactly 299,792,458 m/s, *is* the conversion factor between mass and energy. So one kilogram of mass is equivalent to 89.8755 billion trillion (8.98755E+16) joules of energy. Conversely, one joule of energy is equivalent to 1.111E-15 kilograms (1.111 picograms).
In particle physics, these units are large and unwieldy, so we conventionally leave out the factors of c. We measure energy in units of "electron volts", or "eV" (the energy gained by a single charged electron falling through one volt), and mass in units of eV/c^2. Often, you'll see us write mass in eV (or MeV, GeV, etc.) as well; we "just remember" to stick in whatever factors of c are necessary.
I do not understand c(squared). How can the constant speed of light be squared? "It is what it is". What does squaring do for it? How do you visualize light going faster than light to begin with? Why do you say to "just remember" to stick in factors of c? Light can not ever go >c so how does it square? What does this look like? I wish I could express this better.
@Rigel
squaring "c" has nothing to do with increasing speed of light.. or anything about it's constant. It's due to basic math. It has to do with how the basic formula for kinetic energy is derived and units it has.
Energy = 1/2 mv^2.. How you come to that formula is high school physics, and there are plenty of explanations online, just google "kinetic energy" and classical mechanics.
Einstein used speed of light for "v" term because he reconed that's the speed energy moves with.
I think the person who asked the question was more amazed that the units worked out. Ethan's explanation was nice, but it didn't get at the fact that the SI units are so tightly bound together, which is the reason it worked out. Basically the joule (unit of energy) is equivalent to a kg.m^2 / s^2, so if mass is given in kg and the speed of light in metres per second, it works out just right. If the units were imperial--say, British thermal units for energy, pounds for mass and miles per hour for speed--then the questioner is right that an arbitrary constant would have been needed in Einstein's famous equation.
Um.
Dimensional analysis anyone?
If an equation is giving a result of meters divided by seconds, surely the definition of the result, velocity, must be measured in meters per second.
What else would the result be???
Thank you thank you thank you Michael Kelsey! I've never been able to get that answer from anyone I've ever asked on the topic!
@ Uncle Monty
I think you are right that the person who asked had units in mind as well. The issue is that it's irrelevant to the formula and his question about a constant in the equation.
Units.. SI or whatever have no bearing on the formula which is a relation. There would be a constant there if laws of physics were different in some way, but not on the units you choose do describe them. They do have a bearing on the result, or value in other words. But the formula is the same weather you choose to use yards.. miles..knots.. pounds... whatever unit for whatever measurement... as long as you are consistent. No one says you have to use Joules or meters.. or seconds..
Sinisa, now I'm confused again.
So it would be "the same" even if I used lightyears, gigatons, and grams? What does it mean to be "consistent" in the units I'm using? There's got to be some baseline assumption here as to what units "fit" the formula, right? Surely, there are "right" and "wrong" units to plug in?
You weigh the same no matter if you use pounds or kilos, Dark Jaguar. Just the number representing that weight is different.
There's no such thing as a right number to use for your weight.
@ Dark J
Is the actual physical speed of light any different if you describe it in meters per second, or in miles per hour or.. something else? No it's not. The value is different.. so i.e.
c= 299 792 458 meters / second
c=670 616 629 miles per hour
and so on.. same for everything else. What I mean by consistent is that you have consistency in using them from start to finish.
There is nothing wrong in saying E=mc^2 where m is mass in potatoes, c is the speed of light measured in thumbs per sneeze and e is energy in potatoes weight times the thumb per sneeze squared.
As long as i have consistent values for what I mean by one potato weight, one thumb for lenght and one sneeze for time.
p.s. there is nothing special or universal in SI system, and I have to disagree with mr Kelsey who says that it's due to SI system. It's the same in any system, as long as you have values for time, length, mass, charge etc. defined within one system.
1 meter is defined as 1/10.000.000 distance from equator to pole.
1 gram is defined as weight of water at room temperature in 1 cm ^3 volume.
and 1s was defined before 60's as 1/86 400 of the mean solar day.
Is there anything universal about some fraction of our day or some thing we picked to represent a meter... there isn't. :)
If laws of physics.. and E=mc^2 is law.. depended on what type of units states and people use.. we would be in a big mess :)
@Sinisa Lazarek #13: Your disagreement with is, I think, exactly on target. I chose to answer Dark Jaguar in SI units for convenience, precisely _because_ they are all defined to click together so nicely.
In "customary units" (not Imperial, Uncle Monty :-), the units we use for energy (for example, calories, horsepower, or BTUs) are entirely unrelated to mass, speed, or anything else. So if you foolishly try to compute the energy in BTUs of a stone of flour, using 670 million miles per hour for the speed of light, you are *definitely* going to have to throw in a whole bunch of weird, arbitrary constants.
But just as you (Sinisa), and I, and others have said, those weird constants are NOT PHYSICS. They are just the consequences of humans choosing stupid units and then having to convert between them.
Michael, Imperial gets dismissed for the most ridiculous reasons.
Mostly because nobody knows or cares about metrology and the history of weights and measures.
To start off, I'll HAVE to say that Metric has advantages that can be taken, um, advantage of now we have universal education. And the problem with the discussion of metric vs imperial is that I really DO *have* to say that.
Imperial (as the most well known example of old measures) was developed to be human-definable. The old canard of "How many hogsheads to the chain do you get, huh, huh, huh..." Beavis-and-Butthead style of "proof" of the metric system is therefore evidently rubbish. You didn't measure the distance to London in feet or inches because you used yards (how many strides) or leagues (how long it will take to walk there) to define the distance to London. Hence the odd "conversion". They're odd because the sizes were defined without needing, wanting, or caring, to work out how they convert to each other.
Secondly, being for a pre-literate public is evidenced by their use of non-decimal conversions. 60 or 12 are common. This is because they have a dense number of divisors. Simple integer divisors mean that you can easily work out how to get to the smaller unit: divide it up into even units.
Dense divisors means you can maintain a fine granularity, necessary when selling to the public where they can afford or need a variable amount of the goods.
When it comes to today, all the rubbish about "How many acres to the square mile?" is ridiculous. The only *necessary* reason for the change is that everyone else uses it. Since we're a globe with international connections for every country, interoperability is far more important than being human-scale figures. Since we all know enough maths to work out the decimal system, the easy divisors is moot.
Sniggering over the odd conversions is merely displaying ignorance and arrogance. It's silly and uneducated to go "It's easy to convert meters to kilometers". No it isn't: it's impossible! THERE IS NO CONVERSION. Might as well say that we should keep imperial because it's easy to convert between yard and kiloyards".
"Everyone else uses it" is sufficient reason/
Oh, an addition, the example given would define the unit of define energy in stones per (mile per hour.) squared.
Since BTUs aren't defined as that, you need conversion.
But if Joule had been defined with units in imperial, you'd be making the same chortle over that silly metric system.
I understand that in THAT sense, units don't matter. What I'm saying is, that formula doesn't tell me ENOUGH to figure out what the relationship is between mass and energy, even though that's EXACTLY WHAT IT IS.
I know that I could put the M as either 1000 grams or 1 kilogram, and it wouldn't matter. What I DON'T know, intrinsically, is what the hell I should measure "E" in once I run the calculation. I COULD plug in all sorts of values for C that are all equivalent, but if I use the same unit for mass, I'll end up with a different number as E depending on which value for C I use.
Only by using that kilogram/joule/meter INITIAL value do I even HAVE something I can work with to convert. If I didn't know those, how the hell would I know what E's units "should" be for any given M, or what C's unit "should" be for that matter. With it, yes, I can use whatever units I like, because there's a very simple "conversion ratio", but without it? This is what I'm saying The formula itself does NOT tell me enough.
Quite what you don't get or why that needs to be clarified, I believe, is the problem everyone else is having here, DJ.
In SI units you measure it in Joules. Or Watt-hours. Or BTUs. Or in eV. It doesn't matter. It still has the same energy.
What is your problem here? What are you expecting to "know" when it's explained to you what you don't get?
The formula tells you EXACTLY ENOUGH:
E=0.5 * mv^2
O.5: dimensionless. No units.
m= mass.
v= distance per time.
E's dimensions are, from this formula:
mass * distance * distance / time / time
Now, here's something that'll blow your mind!
E = f * d
f = force
d = distance
So what units would force be in?
dimensional analysis
f = E/d
= mass * distance * distance / time / time / distance
= mass * distance / time / time
Note too that
f = m a
units of f, here?
mass * distance / time / time
WOW! LOOKIT THAT!
Note, too, that the units of force here don't give a flying fig what unit mass, time or distance is in. Neither does the unit of energy care what they are as unit sizes.
So I get back to my original query: what is it you think you don't understand that must be understood?
In short, what the hell else should the formula tell you, and why do you think it should tell you that?
Dark Jaguar: you are correct that the formula does not tell you enough to make it work. What Michael and another less patient commentator are trying to convey is that that formula, PLUS the knowledge that units have to be identical on both sides of the equation AND that a unit of energy can be understood as equivalent to units of mass times units of distance squared over units of time squared IS enough. So you can either use SI where the standard unit of energy is equal to the correct combination of the other standard units, or you can use whatever units you want for two of the three quantities and derive the appropriate unit for the third quantity. If you choose to use BTU and mph, for example, then you'd need to define your own unit of mass so that the numbers worked out right.
I could not find how to “Ask Ethan” so I will do it in the comment section for the latest post. I’ve been banging away all over Internet, trying to get the answer to this question, so here it is:
MIT posted in 2013 a report that they could find no influence of dark matter in the orbits of any of our solar system planets or their moons. Dark matter is everywhere in the universe and affects everything we see – except here. Where is our dark matter? That is not question, this is: Since we cannot detect the affect on dark matter in our local solar system, what is the closest object we can see the affect of dark matter? Andromeda, the Large Magellanic Cloud, local star clusters, where?
And is the distance from earth a correlation to the affect of dark matter? The red shift or velocities of the matter we can see is such that the distance from earth is correlated to supposedly dark matter’s affect?
Since this is suppose to be a science blog, citation is way important and although I do not normally post a web site in an email or comment, here is the MIT post:
http://www.technologyreview.com/view/516681/the-incredible-dark-matter-…
What is the closest object in the universe in which we cannot explain our observation without the dark matter theory?
I suppose my misunderstanding stems from my lack of mathematical understanding.
I've seen this tossed around, but I'm not exactly sure what dimensional analysis actually is. Supposedly, an understanding of this would tell me exactly how to, as you explained, "define your own unit of mass so that the numbers worked out right". But, I don't know how to make the numbers work out right, I guess. That's what I'm missing. Thanks for the description of E and all, but I feel like I'm still missing some fundamental understanding, some basic underpinning of math at that level that I just never learned.
(My school never taught me dimensional analysis...)
Look, what is it you expect to know that you think you do not know now?
Forget dimensional analysis (senior high school-level physics, 6th form in the UK), the post I gave showed you what it does and means, so if you're still in the dark, it's not going to help.
Step back.
Ask yourself "Do I not understand something, or do I understand but thought there was more to it than this?".
An example is a conversation I had with a contractor about CGI programming. He wanted to know what it was, what he needed to know and look for. I said "The URL contains the values input into the web page that it uses to calculate what HTML to print out.".
"Is that all?" he said.
"Yup".
"I thought it was difficult!" he says.
"Nope, it just has an acronym so it sounds cool and different".
If you think there is something missing,what the clucking bell do you think it is? What are you expecting to be able to do when it's explained and you understand that you find yourself unable to manage now?
Until you answer this, you're not going to be able to be helped because nobody, not least yourself, knows what the hell is wrong.
uncleMonty, maybe you can say what is meant by work when you say "the formula does not tell you enough to make it work."?
E=mc^2
contains everything you need to make it work for any given mass, m, when the defined speed of light is input.
What is not working there? What does it mean to say "work" that you find missing in it when you claim there isn't enough information for it to "work"?
Everything is needed there for any given mass, all that's missing is the speed of light in vacuuo, which is a constant in ANY system of measurement. Not the same one, but a constant.
I mean, is that what's "missing"? The speed of light? Because you find that with a measuring device. Calibrate it to your system of measurement, and bob's your auntie.
Dark Jaguar: here's an example of how you'd figure out your own units. Say you measure distance in feet, time in minutes, and mass in kg. Energy is (by its definition) expressible as mass times distance squared divided by minutes squared, so if you define the unit "1 Jag" equals 1 kg.ft^2 / min^2, then Einstein's equation will come out just right with no need for a constant multiplier.
If you find, in whatever choice of units you could come up with, that you need a constant multiplier for Einstein's equation to be true, that constant will be related to the conversion between units. If for example you used an AltJag as your unit of energy, which is equivalent to kg * ft^2 / sec^2, then you will need a constant multiplier of 1/3600 (or 3600, depending on which side of the equation it goes) which is the conversion factor between seconds squared and minutes squared.
Wow, I said it right there in my message: what's missing (for Dark Jaguar) is the knowledge that there's such a thing as dimensional analysis and the ability to carry it out. Were you born with that knowledge? Whether you think that knowledge is just plain common sense or is something a person needs to be taught is irrelevant; the fact is that demonstrably Dark Jaguar has the formula and that plainly is not sufficient for him/her to figure out the units. What *is* sufficient is the combination of the formula and the knowledge of how to carry out dimensional analysis, or the knowledge that energy is mass times distance squared over time squared. (And even you wouldn't claim that that knowledge is just common sense.)
@ UncleMonty
" then you will need a constant multiplier of 1/3600 (or 3600, depending on which side of the equation it goes) which is the conversion factor between seconds squared and minutes squared."
Now I think you're missing the point :) If you use kg ft/sec... instead of kf ft/min... you DO NOT NEED any constant or any change to the equation!! Not in E=mc^2 or anywhere else. The formula is the SAME. The result is different. One result will show the energy in terms of minutes, the other in terms of seconds, BUT THERE IS NO RIGHT OR WRONG value, it depends on you and you alone.. what are you asking the formula to calculate, minutes or seconds.. jules or volts or meters.. The formula doesn't change, the input values do. Come on guys, it's common logic.
When we talked about the question in the original post, and constants in formula, I think the spirit of the question (not Jaguar's.. but original one) was why aren't there any constants i.e. Pi, or plank's constant or e etc. Not about converting between minutes or pounds.
@ Dark Jaguar
"What I DON’T know, intrinsically, is what the hell I should measure “E” in once I run the calculation"
In whatever the inputs were in. That's what we are trying to explain. If you've input the mass in tons,length in knots and time and lunar years, you would get a certain result for E, which doesn't have any naming unit, but is perfectly valid. It's up to you to to pick units, really. A bunch of guys came one day and said.. ok we are gonna name a unit of energy Joule, and we will express it in kgm^/s^2. It's just an agreement of people. Nothing in terms of physics or math.
----
"What I’m saying is, that formula doesn’t tell me ENOUGH to figure out what the relationship is between mass and energy, "
IMHO I don't think the issue here is with units. Units won't tell you anything. The issue is you need to study SR for a bit. To understand why E=m because that's the point. Speed of light is actually a constant in the equation. Why is E=m you won't find in units, you have to dig into theory :)
Nope,you said this:
I asked for the definition of "work" used there.
"Dimensional analysis" doesn't mean anything. I'd said before what it was, but DJ still didn't see anything fixing their confusion. Moreover, dimensional analysis doesn't say what's wrong with the equation, what's missing. NOTHING IS MISSING.
You get energy out if the equation mc^2. Assigned to a variable, E, it's stated as:
E=mc^2
Dimensional analysis tells you what the specific units of E are, but then again, you don't need them. It's ENERGY. You will note the unit of energy is the Joule. Not the kg m^2/c^2. JOULE.
THIS may be why DJ isn't "getting it", though. People are using what they think in their head, writing down the result, then assuming that the bit they think is "obvious, surely there's no need to explain that", WHEN THERE DAMN WELL IS.
DJ in his "I don't get it"
You in your "Dimensional analysis".
I made the engagement that it was "what units of measurement would result?" but if that had been so, DJ would have at least moved on from "I don't get it".
Sinisa: no, actually *you* missed *my* point... you definitely *do* need a conversion factor if you measure time in minutes and energy in kg * ft^2 / sec^2. That was my point. To you, it is perhaps self-evident that you shouldn't do that. But to the average person on the street, assuming you can find one who actually can name a unit of energy, ask them for a unit of energy, a unit of speed and a unit of mass. Bet you 10:1 they won't end up giving you a consistent set of units in the way required by dimensional analysis. (Of course, the constant "1/3600" is not really dimensionless: it is 1/3600 min^2 / sec^2.)
If your unit of length and/or time are such that the speed of light is definitionally equal to 1, then
E=mc^2
becomes m * 1 * 1 = m.
Because c is a constant, just like 1/2 is a constant when you calculate kinetic energy. Like any constant, if it is 1, you don't have to write it.
E=m
Is only confusing because you've dropped the information that the speed of light (a constant) has been dropped so you can cut down on the visual clutter of the equation.
This is why that equation is never used.
The equation is only important in explaining that you can refer to masses in terms of energy. The rest mass of an electron can be expressed as 511keV.
(note I'm working off SL's ending comment under the assumption that "the equation" you, uncleMonty and DJ, were talking about, BUT NEVER SAID, was E=m. And in that case, as SL says, dimensional analysis is the OPPOSITE of what you need: because you've mathematically dropped a constant that has dimensions, but no mathematically significant value)
NO YOU DO NOT
The unit of energy in this case would NOT BE THE JOULE.
If you DID want it as joules, then yes you would need a conversion factor, just as you need one to turn from joules to electron-volts.
HOWEVER that "need" only arises because you created the demand that the result be expressed in a different metric system.
SL DOES NOT need to add a conversion factor, the energy will be expressed in *different units*, but those units *would not require a conversion factor*.
This is a problem with the dismissal of the "Silly" Imperial measurements farting on and on about "how man chains to the furlong, huh?". When the gripe has been about "converting from one system to another", it's inevitable that it will be used as a hidden assumption where it no longer applies.
Wow, you insist on a deliberately antagonistic reading of my posts. It is clear that when I say the formula does not work on its own, I mean it does not work on its own for someone who expects to simply put in a numerical value for E, another for M, and another for c (then square it) to be able to verify the equation. In the very next sentence I gave this very explanation of what I meant by "the formula does not work by itself", but since you demand it again, here it is.
We could also add that a reader can only understand the formula if they know what E, m and c refer to, or what the "squaring" operation means, or any number of other things you take for granted, but since those is not Dark Jaguar's problem I left them out as he/she seems to want to know about the units working out correctly.
I can't edit my posts above so let me make a correction here which might have led to Sinisa's attribution to me of an error: I wrote that energy can be shown to be in units equivalent to mass times distance squared over minutes squared. I meant mass times distance squared over time squared of course.
Mixed up.
SL was saying that you don;t HAVE to express energy in "per second squared". If your measures are all per minute, YOU WOULD NOT DO THAT. You'd define energy in "per minute squared".
Yes, if you were dumb enough to measure time in different units from the system you measure energy in, you need a conversion factor, why the heck would you do that, though? I might measure the time over several minutes, but I'd use the units of seconds.
I wouldn't convert the result of mc^2 to account for using the wrong damn unit of time, I'd convert the value of time BEFORE USING IT TO DESCRIBE VELOCITY.
@ UncleMonty
"you definitely *do* need a conversion factor if you measure time in minutes and energy in kg * ft^2 / sec^2."
yes, in that case you do. But that is exactly what I meant, when I said "you need to be consistent". If you choose to pick meters for one value and yards in another value, of course you need to convert. But formula doesn't care about that.. formula remains the same. In principal, you are correct.. you could alter the formula to compensate for conversion.. but you never do that. You always do conversions before input. That's what I said by common sense.. and not that it's obvious to me.. if society did that, then all of us would learn different formulas depending on the naming system our state used. instead we all learn that a^2+b^2=c^2 .. and none of us would really think to input meters for a and miles for b and expect c to work :D
/uncleMonty, it's clear you know what YOU think you're thinking, but it is ALSO clear that you think that it is clear in what you write.
IT IS NOT.
see this. Your opening statement, I have bolded the appropriate part:
No, you do NOT approach an equation like
E=mc^2
*then fill in all three values*.
In what sense is the equation necessary when there's nothing left to write in? An equation is written to find an answer, and your "it doesn't work" HAS NO UNKNOWN.
No wonder it doesn't work for you!
I'll boil it down for you very simply. Your statement there is like being asked to answer the following question in school:
If a man is 75kg in weight, how much does the man weigh?
If you then say "That's a dumb question", then you've discovered why it doesn't work. You've also found what's wrong in what you state categorically is "It is clear" is CLEARLY wrong.
It CANNOT be what you meant, since the description is nonsense.
Which takes me back to my opening statement: you may know what you're thinking, but it's not what you're writing.
Wow, this is entirely uncontroversial. I wrote that if you don't use consistent units for mass, energy and speed, then you will need a conversion factor. As in, this equation is correct:
100 kg x (3x10^8 m/s)^2 = 9 x 10^18 J.
But this:
100 lb x (3x10^8 mph)^2 != 9x10^18 btu.
is not correct despite the same numerical values (obviously). If you want to express mass in pounds, speed in mph and energy in btu then you will need a conversion factor.
I say again: to most people, if you ask them for a unit of speed, a unit of energy, and a unit of mass, they will most likely not give you a consistent set. You can say "always use a consistent set", and of course that's the proper way to do it, but the fact is someone can use whatever units they want, if they also apply a conversion factor. It is natural for such a person to wonder how come they don't need to multiply by some other quantity when they use the SI units. To you the answer is obvious. I'm trying to explain it to a person for whom it's not obvious.
Wow, it's not that I expect anyone to be approaching the formula knowing all three values (though you might want to verify that experimentally-determined values match expected values, in which case you'd have three values in hand). But if you know two values, you can get the third in whatever unit you have in mind, if you have the correct conversion factor.
Nope. You didn't. You talked about first of all dimensional analysis, which doesn't give a fig about units. It doesn't USE units. It uses fundamentals. mass. Not kilogrammes, not pounds. MASS. It uses Length. Not meters, not inches.
You THEN went on in response to SL's accurate post to talk about how SL was wrong, that you DID need a conversion factor, but left out that you had NOT been consistent in your units.
Indeed SL's follow up post points out that HE knew what you now claim "is uncontroversial" (which it is) "I wrote that..." (which you didn't).
AGAIN, coming back to my point I've made three damn times now, you may absolutely be clear IN YOUR OWN MIND that you know that, BUT YOU ARE NOT WRITING THAT DOWN.
YOU CAN NOT complain that people are getting what you *mean* wrong, when you aren't actually saying what you mean.
You have to say what you mean first. Even if it's wrong, it's far less wrong than "thinking" the right thing, but *writing* the wrong one.
Sorry about the missing slash of the closing tag there.
For the insanity of the "pah! imperial system needs conversion!" have a look here:
https://www.unc.edu/~rowlett/units/cgsmks.html
Appropriate quote for people
See also "erg", "Angstrom", "barn" and many many more.
I give up Wow, you can have the last word, this will be my last post on the topic. I hope you can calm down, it is upsetting to imagine someone as angry as you. I believe that for some people, confusion about why the units work out is at the root of the problem. You can see as much in Dark Jaguar's first post in the thread. The fact is, if you use inconsistent units, it's true that you will need a conversion factor for the numerical result to be correct. Naturally, someone who understands the issue of consistency among units, like you or SL or Michael, will have no trouble with the issue.
p.s. I did not leave out, as you claim, that I was being deliberately inconsistent in the units for my post #25. Read it again and note sec != min. I understand you may have missed it, by reading too quickly and jumping to conclusions, but I was explicit about the units not matching.
As to your claim people won't use consistent units, I beg to differ.
Measure out a field for football or whatever. Ask how big it is, and they'll say "so many meters by so many meters" (or yards). Ask them the area, and they'll say "So many square meters" (or yards).
They won't say "so many meters by so many feet" and then "So many khatha" in answer to the query of the area of that space.
And when tasked with a maths or physics question to work out an equation, as SL says, they convert "x minutes y seconds" or "a hours b minutes" into seconds first, THEN use the value in the equation. Assuming, of course, they're given a question where they've used different units in the description. Which I'm pretty damn sure nobody has ever seen in school (well, maybe several decades ago).
Oh cry me a frigging river unclemonty. I guess you never looked at your mistakes, just looked how much a meanie I'm being to you and then decided that you shouldn't have to put up with the bruise to your ego, so didn't have to read anything at all.
It's a logical fallacy:
http://en.wikipedia.org/wiki/Appeal_to_motive
IOW I'm just being mean, so you don't have to face the substantive claims.
And then you flounce off so you don't have to answer if you don't see a way to find a way out.
Oh, and though uncle has cried off, please note uncleMonty has committed another logical (propositional) fallacy:
Affirming the consequent – the antecedent in an indicative conditional is claimed to be true because the consequent is true; if A, then B; B, therefore A.
In this case: you need conversion factor because if you don't use consistent units, you need a conversion factor.
Something SL tried to point out too.
@ Uncle & Dark
here's Dark original question.. " I thought “Okay, but what if I use the wrong scale, like I see “E” as a single photon, and “M” as a metric ton? What units do I plug in here?!”."
depends what you want to calculate? you didn't say that. How much energy does a photon need to have a "mass" of i.e. 1 ton.. Or do you want to calculate how many metric tons does an average photon of visible light have?
E of photon = ?
if m in tons.. let's say 1ton
c in whatever value units you have/use.. 300.000km/s.. meters..
.....
Thanks for that SL.
Unfortunately it looks like it's so confused there's really an intellectual gordian knot gone wrong.
E is a photon. And you know it's energy. You don't know its mass, so you rearrange the equation:
m=E/c^2
Put in the energy of the photon in your chosen unit, convert to the mks system so you can relate it back to the weight you want in the mks system (assuming metric rather than imperial or long ton), put the velocity of light in there twice (convert to the same unit system, mks).
Result is in kilos (mks system again, remember). Divide by 1000 to get it in tons instead.
Done.
Everything is there: use the same unit system is all that's "missing", but that's not really missing in any other sense than when you speak to someone in your native tongue, you're "missing" a translation to another language if they have a different native tongue.
You wouldn't expect to get sense out of someone speaking russian to you if you don't understand russian, so why would you expect to get an answer of a question when you've changed the system of measurement?
Oh and "a photon" isn't a scale of energy.
Unfortunately confusion abounds. Possibly because DJ is trying to make it harder than it is. Either because they think "This is physics, it MUST be hard" ,because they want to make out that *ordinary* people wouldn't understand,or because they're JAQing off. In descending order of politic to DJ.
Wow, do I really sound like I'm crying off to you? You are congenitally unable to have a disagreement without ranting, it's just so tedious after a while. I can sense the spittle-flecked keyboard and your redfaced stupid-old-man anger from the other side of the internet (really, do you want to expand this to a rant about good old imperial units now? You're responding to arguments from the voices in your head--no one else brought that up). Read Dark Jaguar's first post again: this an example of a person not knowing what units to use, and being explicit about that. Go and ask the kids on your lawn--if they're not too afraid of you by now--what they think are appropriate units for speed, energy and mass: I bet they won't be consistent. Your boneheaded ranting about "what is there not to understand" notwithstanding, it may be possible for someone not to know that units need to be consistent for this equation. Thus, explaining this to them with examples they can understand might help, instead of spewing your tedious why-is-everyone-so-goddamn-STUPID schtick in almost every thread on this blog. You are the very reason the internet sucks.
Everything that's necessary to calculate E is already present in the equation. As arguable as it is, the formula is absolute until some other scientist discovers a new elelment for the formula that has actually been missing this whole time.
Science is progressive and E=mc^2 is what has worked until now in accordance to the theory that has been corraborated and in that theory there are no other constants than the ones present in the formula now.
u15085504
"The equation is only important in explaining that you can refer to masses in terms of energy. "
the vice versa part was always more interesting to me. It's not only a seemingly perfect relation, but it's an eye opener for energy as well. I mean, before that, noone in their right mind thought that i.e. a magnetic field has mass. or any energy or field... two worlds.. matter.. "real stuff".. and forces... relativity showed that they have same roots. Not only conversion of values.. but a relationship of the nature. Because of that, you can i.e. talk about a gravitational force between two energy fields.And that's just awesome :)
Not just magnetic fields,
Spinning is energy of motion and produces "more mass".
It's a good point to make out, a good theory has consequences that you can test. Relativity makes the above test and it too can be shown to be correct. Even though it shouldn't follow from any of the competing theories. Which makes the prediction a good discriminator of this theory from the competing ones.
This is why falsifiability is so important to science (though not as essential as some popperian proponents make out). If you can't tell the difference between two theories, there's a problem in the theories.
And there's no point to a "disagreement". All that is is an excuse to have a row. Unless you meant here "argue", which has the intent that some agreement is on the table.
Though admission (even if inadverdent, a la freudian slip) that you don't want agreement or progress is quite accurate for you. If you'd ever read the content rather than throw hissy fit over how mean I am, you'd be able to see that you're NOT clear, even though you insist "it clearly meant....".
You also insisted that SL was wrong, never accepting (reading?) his point that not only do you have to keep your units consistent, everyone does. Because you thought "you need conversion factors" when the entire pigging POINT is that you don't here. If you pick your unit scale appropriately, there's no need.
UNLIKE, for example, the description of the radius of a circle to its diameter. There is NO UNIT SCALE you can invent that won't need the value pi to include.
Which was the point of Ethan's post too.
The problem you had was you had an idea and never stood back to look at it. Therefore anyone pointing out something you hadn't noticed "did not understand" what you "clearly meant".
As the E=MC2 equation is derived based on the assumption of a particle assumed in vacuum or space travelling towards the edge of the box and back to the position. I think if the assumption is considered about an explosion with liberation of energy where at a single point of time different forms of energies are liberated like Heat, Light, Vibration..etc. As per the law of conservation energy energy can neither be created nor destroyed from one form to another but here we usually observe that at a single point of time, we tend to observe that one form of energy can be sensed or seen first than the other which gives the perception that one is liberated later than the other. Here what i was trying to know is that when some amount of energy is liberated is itself released in different forms at a time which gives me a thought that when E=MC2 and the liberated energy is itself released in different forms, can it be considered as a partial mass getting converted in to one form of energy where as the other partial amounts of mass into other form of energy. If the following assumptions are considered as true then how should we calculate the Energy for the whole energy liberation as per E=MC2 and law of conservation energy Should we consider the different forms of energies each as E=MC^2 by dividing the total mass equally by no of forms of energy liberated to get the partial masses, as knowing the accurate mass conversion into different forms is not possible and then apply the mass for each equation for number of forms of energies liberated or should we consider only the Mass of the matter before the liberation of energy and multiply it with C^2 .
Not your fault, but that's extremely hard to read. Not your native tongue. Try smaller statements, or at least spread the words out with blank lines separating the thoughts.
You can take the rest mass and add the energy divided by c^2 to that mass to get the relativistic mass of all included energy constituents. That's what E=mc^2 means.
If you release energy and let it leave, the remaining relativistic mass will reduce by that energy divided by c^2.
If you lose relativistic mass, then energy will have been released and that energy will be given by the change in mass multiplied by c^2.
Thank you for the explanation @Wow.
I felt that i have received an apt answer for my doubt but please go through the example and kindly suggest me that whether the approach be in this way.
Example:- If we assume matter of 3KG'S is burnt and want to calculate Energy applying E=MC^2 then the usual solution will be like the below mentioned.
M=3KG'S
C=29979248
then
E=3*sqr(299792458)
Ans=269626553621045292.
Now if i apply my thoughts mentioned above by considering that the energy is liberated at a time in different forms like heat, light etc to the above example the solution would be like this.
Considering M as total mass and m1, m2, m3...m(n-1),...m(n) etc. and then dividing it by no of forms of energy say for example 6 forms of energy is liberated.
ie. 6/3=2 now substituting that 2 in E=MC^2
i.e 2*sqr(299792458)
we get 179751035747363528 now if we substitute this for each form of energy that is 179751035747363528*6 or E=m1c^2+m2C^2+...+m6c^2 the result would be 1078506214484181168.
By the explanation of the above mentioned examples what i wanted to convey is that by directly applying E=MC^2, which is derived using relativistic equation that is mass and energy equivalence, we are only considering the mass-energy equivalence relation of the matter before energy liberation like 3kgs in the above mentioned example.
but the method i have mentioned below that is dividing the Total mass of the matter by the no of energy forms liberated gives the details of partial masses conversion into different forms of energy.
As it is not possible to know the accurate amount of partial masses conversion in to accurate of amount and type of energy, i have divided the total mass of the matter by no of forms of energy liberated.
Each form of energy liberated from the 3KG'S of mass by conversion of external heat energy used to ignite the matter to convert the heat energy into chemical,heat,light energies etc. during combustion. Each form of energy liberated simultaneously was assumed to be possessing the converted partial mass m1,m2,m3..ETC. with c^2 velocity.
Total Energy=Sum of partial masses multiplied by velocity of light squared converted into different form of energies.
If expressed in the for of equation:
(partial mass)m=M(Total mass)/no of forms of energy
and
M=m1+m2+m3
C=c(1)^2+c(2)^2
that is
E=m(1 suffix)c(1)^2+m(2)c(2)^2....m(n-1)c^2(n-1)
E=MC^2
By following this process i am getting a difference of about 10% more than applying direct formula E=MC^2..
Kindly share your opinion.
Thank you for the explanation @Wow.
I felt that i have received an apt answer for my doubt but please go through the example and kindly suggest me that whether the approach can be the following way.
Solution 1:- If we assume matter of 3KG’S is burnt and want to calculate Energy applying E=MC^2 then the usual solution will be like the below mentioned.
M=3KG’S
C=29979248
then
E=3*sqr(299792458)
Ans=269626553621045292.
Now if i apply my thoughts mentioned above by considering that the energy is liberated at a time in different forms like heat, light etc to the above example that is Solution 1: the solution would be like this.
Considering M as total mass and m1, m2, m3…m(n-1),…m(n) etc. are the individual masses of M and then dividing it by no of forms of energy say for example, 6 forms of energy is liberated during the combustion of the 3KG'S of matter.
ie. 6/3=2 now substituting that 2 in E=MC^2
i.e 2*sqr(299792458)
we get 179751035747363528 now if we substitute this for each form of energy that is 179751035747363528*6 or E=m1c^2+m2C^2+…+m6c^2 the result would be 1078506214484181168.
By the following explanation and examples mentioned above, what i wanted to convey is that by directly applying E=MC^2, which is derived using relativistic equation, that is mass and energy equivalence, we are only considering the mass-energy equivalence relation of the matter before energy liberation like 3kgs in the above mentioned solution 1:
but the method i have mentioned below the solution 1: that is dividing the Total mass of the matter by the no of energy forms liberated gives the details of partial masses conversion into different forms of energy.
As it is not possible to know the accurate amount of partial masses conversion in to accurate of amount and type of energy, i have divided the total mass of the matter by no of forms of energy liberated.
Each form of energy liberated from the 3KG’S of mass by conversion of external heat energy used to ignite the matter to convert the heat energy into chemical,heat,light energies etc. during combustion. Each form of energy liberated simultaneously was assumed to be possessing the converted partial mass m1,m2,m3..ETC. with c^2 velocity.
Total Energy=Sum of partial masses multiplied by velocity of light squared converted into different form of energies.
If expressed in the for of equation:
(partial mass)m=M(Total mass)/no of forms of energy
and
M=m1+m2+m3
C=c(1)^2+c(2)^2
that is
E=m(1 suffix)c(1)^2+m(2)c(2)^2….m(n-1)c^2(n-1)
E=MC^2
By following this process i am getting a difference of about 10% more than applying direct formula E=MC^2..
Kindly share your opinion.
Yes, you get about a 10% error in your calculation because the difference between the sum of the squares and the square of the sums is about 10%.
Your mathematics are in error.
Ye it's is square of sums and it's not my mathematics error. What I was trying to know is that the whole energy liberated also consists of different forms of energy which is the resultant of different partial masses of the same matter getting liberated.
Each form of energy is E=MC^2 , if we ignore the partial masses and different forms of energies and directly multiply mass by velocity squared we only get the total mass getting converted.
By dividing the total mass by no of forms of energy , we are getting the individual mass conversion which are again substituted in the no of forms of energy , which give the sum of individualistic masses making up to total energy.
Why i am saying that it's not the error of my mathematics so confidently because in physics and chemistry we use this approach for example Dalton's law of partial pressure where we calculate individualistic pressure and the pressure is also a form of energy.
The reason here for dividing the total mass is to know the individual mass conversion as there is a perfect realistic fact that different forms of energies are liberated from every energy conversion that means the total mass is getting divided as there is no other mass or energy getting newly involved.
It's only the mass of the matter which is resultant in different forms of energy.
Don't the ignorance of this fact make the difference in measuring the actual amount of energy contributed by each form of energy
I am sorry for mentioning pressure as a form of energy. Only consider the principle of Total pressure but not the pressure as energy.
@ Krishna
I might be wrong because your English is a bit hard to follow, but i think your assumptions are wrong.
First thing.. you can't talk about E=mc^2 and burning wood or coal. Burn 3 kilos of wood, and you will get 3 kilos of ash more or less + some gasses. It's conservation of matter. And the energy you get by burning 3 kg of wood IS NOT mass of wood x c^2.
I'm not a chemist, but maybe only some tiny fraction of a percent (in case of combustion) is a direct transfer between mass of fuel and energy released. The rest is just plain chemical reactions which have a certain % efficiency.. hence in most cases there is no "missing" mass or missing "energy" that got converted directly through E=mc^2.
But if you wanted to know how much energy would be released if you split every single atom in that 3 kg of wood, then you would use relativity.
p.s.
or in reverse.. if you burned 3 kg of wood and measured the ashes, water vapours, other gasses, heat used, heat produces etc etc and you could account for everything, and you still find i.e. 0.0000001 grams missing somewhere... that's the equivalent of E=mc^2.. that's the ammount of matter that got "converted" to energy and was imparted maybe to some photon or caused some heavy elementary particles to be created and decay.. etc..
And that's why you're getting the error and are confused. You think you know what you're doing but you definitely 100% do not.
With Dalton's law, you don't have squares of the magnitudes you're adding together. You do with your treatment of energy.
SL's point is well made too. You don't get full liberation of the mass in a merely chemical reaction. it's a millionth of the value of nuclear reactions, which is a tiny fraction of a percent of matter-anti-matter annihilation where the entire mass is converted to energy.
Either you're faking knowledge, trolling, or incompetent at this.
V.Chaitanya Krishna:
No that would not work. Matter to energy conversions must still obey conservation laws. The total system has to end up with the same kinetic energy and same momentum it started with, and must also obey any other conservation laws that may be relevant (conservation of charge, angular momentum, etc.). This means that the joules released can only be emitted as certain types of energy and in most cases the amount for each type is directly calculable as the system is not free to vary anything.
This, btw, is one of the reasons mainstream nuclear physicists and radiochemists are so skeptical of cold fusion claims. You can't just arbitrarily claim that 'for this nuclear reaction the energy comes out as kinetic motion rather than gamma rays.' Depending on the reaction, that claim is very likely going to violate all sorts of conservation laws.
OK @Wow lets us for the moment assume that i am 100% not aware of what i am doing.
I agree that there are no squares involved in Dalton's law and it is usually applied for knowing the total pressure in chemistry and linked to physics and can not be applied for squares.
In-fact i did not apply Dalton law or pressure postulates here, but i mentioned that it is similar to the concept i applied and just wanted to make my thoughts understandable to others by comparing my approach with similar concept.
Can you please theoretically explain that why i should not calculate partial mass or mass fraction that is getting converted into different forms of energy.
or can you explain me that why i should not calculate individual forms of energy and sum them, as they are part of whole energy liberation.
Tell me which part of my following concepts are incorrect.
1.Energy liberated during conversion exists in different forms.
2.Mass is getting converted into different forms of energy.
3.All those energies are the Sum of of Total energy liberated.
If you can theoretically explain that my concepts mentioned are incorrect instead of saying that my mathematics are incorrect and i am faking my knowledge, i shall get a better picture and can make corrections.
Then why did you claim your proof of your correctness based on applying its postulates here?
Your maths is incorrect.
I note that you haven't bothered to listen to eric or SL, limiting yourself not to what you are thinking but to what you are doing.
Your thinking is in error too.
Is nonsense. Therefore this:
Is not what you do.
@Sinisa Lazarek
I didn't say to assume about the burning of coal or wood. I just mentioned that assume a 3KG'S matter is burnt, of course to explain that my assumption about 3kgs of mass liberating energy.
and of course E=MC^2 is applied for the total mass of wood or any other matter, its not about the chemistry i am discussing here. I just mentioned the Dalton's here to explain the similarity of the concept but not at all to discuss chemistry.
http://www.emc2-explained.info/Emc2/Equation.htm#.VQLiizSUf3g
Please go through the worked example mentioned in the following link under sub heading named Solving Basic Equation:
Which shows the calculation of 1KG of mass * (3*10^8 ms^-1)^2 in SI units.
I know that if you burned 3 kg of wood and measured the ashes, water vaporous, other gasses, heat used, heat produces etc etc and you could account for everything, and you still find i.e. 0.0000001 grams missing somewhere… that’s the equivalent of E=mc^2.. that’s the ammount of matter that got “converted” to energy and was imparted maybe to some photon or caused some heavy elementary particles to be created and decay.. etc.
I am not saying that we can find the accurate mass conversions, i also mentioned that it is impossible, what i am trying to say is that while calculating the energy we are not considering the different forms of energies which co-exists in the total energy individually and i think that it is important to consider each form of energy individually because those all together with mass and velocity equals E as per the relativity equation.
I am not saying that we can find the accurate mass conversions
You're not even attempting to do so.
After whatever "liberation of energy" you're blubbing on about with the "three masses", they won't be 1kg each after the liberation.
Do you know why?
Because you created the idea that the entire rest mass energy of a 3kg mass would appear in six forms,of which you didn't account for in either type or source.
In short your points have been worthless babble from an ignoramus with a severe case of dunning and kruger.
Your posts are not on topic and are so malformed as to be nonsense, and not due to a language deficiency, the ideas and maths behind them are grotesque parodies of actual thought and rigour.
If anyone else tries and you fail to get their point, then please move to the dump thread for offtopic discussions that are going nowhere.
@ Krishna
"I just mentioned that assume a 3KG’S matter is burnt, of course to explain that my assumption about 3kgs of mass liberating energy. "
and I said, your assumption is wrong. Burning doesn't transform atoms to energy. Burning doesn't "liberate" energy through E=mc^2.
Also, as Wow and Eric pointed out, you also can't assume that different energies or forces in the system contribute exactly 1/n to the overall energy of the system. If that were the case then all forces in nature would be exactly the same strength. They are not.
So what are you asking? If you want to calculate how much heat is released if you burn x amount of something, you don't use relativity, you use thermodynamics. You want to calculate how much energy is released in chemical bonds, you don't use relativity. How much pressure something exerts.. again, no relativity. You can't just put E=mc^2 in any physical systems that generates or uses energy and say.. well.. there are 4 constituents here so i.e. the heat energy component is 1/4 of mc^2..
A simple division of total energy / forms ignores the constraints put on the system by conservation laws. We actually already know far more about what forms the energy must take than this. For example, we can calculate precisely how much of the released energy can go into kinetic (translational) energy because mv^2 of the final system must match mv^2 of the original system.
Well then you have no reason to worry: scientists do consider all the different forms energy can take when mass is converted to energy, and our modern understanding of reaction dynamics is much more advanced, detailed, and quantitative than your proposed (total energy released) / (available forms) = average energy/form. Our understanding certainly isn't perfect and I don't want to leave the you with the impression that we can perfectly calculate were every single eV goes for any potential reaction you can write down, but we are already much more advanced in our understanding than what the type of analysis you propose doing would tell us.
Lastly, for a lot of nuclear reactions we have empirical data on where the energy goes. It would seem silly to calculate an "average/form" for those reactions where we've already done the experiment. On the other hand, if you want to proceed with your plan, I would suggest that you pick a few simple nuclear reactions, do your calculation for them, and then look the data up on those reactions and see whether your analysis got it right or not. If it did and you can show that your technique can be used to accurately predict reaction dynamics of known systems, then people might be interested in using it on unknown systems.
VCK is trolling, lads and lasses.
Just ignored the calculations in their post and they started off with
E0=3c^2
then postulated that there are 6 forms of energy when "burning the 3kg mass", which they don't explain, but the next step is to calculate:
E1=2c^2
then, by claiming this was the energy of each of the "six forms" comes to a total of
E2=2c^2+2c^2+2c^2
Why is unsaid, and nonexistent in any case.
Then claims that this is 10% higher than it got, by an unidentified version of the earlier calculations, however no such figure exits that's 10% lower than 6c^2.
So a complete drive-by trolling.
That should have been 12c^2, not 6c^2.
@Wow
I am not assuming 6 as constant. It's was just an example of forms of energy released from the assumed system. Insted of 6 i should have explained that assume n is the representation of the forms of energy.
Let me explain clearly:
If I assume 3kgs of mass for which energy has to be calculated.
N= Different forms of energy that co-exists.
For example in an energy conversion there are different forms of energy which all together make up total eneergy.
If in case in this 3kgs of mass liberating energy E. With individual energies that is e1,e2...etc. From which I assed that the following 3kgs mass is liberating energy in 6 forms. If for example a another x or y mass liberates energy in 12 forms then we should use 12 . If it is 2 then we should use 2.
That's what I meant tried maximum to explain it in a better way hope my sentences are understandable
@wow
Anyways i am not making an unnecessary argument. It turned into an argument because you didn't get the concept iam trying to explain. I agree that it is not clear due to the language barrier
and a little due to your wrong perception.
Concepts which are unfamiliar or dose not make any sense to you are nonsense for you but not to others who can understand it.
I would like to thank @eric @wow nod other respondents who discussed with me. Eric gave me a great explanation that the science applied at present is much more advanced and the concept I proposed would be insufficient which fulfilled the purpose for posting the whole thing and thank u Eric for guiding me the area to be worked more by taking the data of nuclear reactions .
Sorry, Its and not nod others.
@Eric
Is it possible for you to give me few sample calculations or sample nuclear data such that i can try and check.
Go and assume it on the dump thread:
http://scienceblogs.com/startswithabang/2012/09/23/weekend-diversion-yo…
@Wow
I am really sorry I have gone through the threat. I am new to this blog so I don't know about the thread. Thank you for the information.