I was struck by this paper that came out in the Journal of Child Neurology, looking back at previous study of mercury levels in autistic children. DeSoto and Hitlan looked back at Ip et al. 2004, a case control study that compared the blood and hair levels of mercury in children with autism to those in children who didn't have autism.
The Ip et al. study found no statistically significant increase in the levels of mercury in the children with autism as opposed to the children without. However, on further analysis the DeSoto and Hitlan realized that Ip et al. had made an error in calculating the p-value, and the difference in blood mercury means between groups was marginally significant.
To wit:
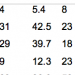
In 2004, Ip et al. reported that no relationship existed between mercury blood levels and diagnosis of autistic spectrum disorder among a group of children with an average age of approximately 7 years. While attempting to estimate the effect size based on the Ip et al. statistics, we realized that the numbers reported by Ip et al could not be correct. The means and standard deviations reported in the 2004 article yielded an easily significant t value (autism mean = 19.53 nmol/L, SD = 5.6, n = 82; control mean = 17.68 nmol/L, SD = 2.48, n = 55 gives a t = 2.283, two-tailed P = .024 or one-tailed P = .012). Ip et al. wrote that the P value was "(P) = .15," and that their data indicate "there is no causal relationship between mercury and as an environmental neurotoxin and autism." After the error was brought to the attention of the authors, a new analysis was conducted by the original authors and they found the original t test to be in error and the P value to be a mistake. Based on their corrected analysis, the authors report the revised P value for their t test to actually be P = .056. We disagree on several grounds that these data indicate no significant effect exists, and report on a completely new reanalysis of the original data set. (Citations removed.)
Fundamentally, this is an argument about whether it is appropriate to use a one-tailed or a two-tailed t-test. Traditionally, a two-tailed t-test with a p-value of .056 would not be considered significant, but does that really indicate that no significant effect exists? Particularly, the use of a one-tailed t-test is justified in cases where a reasonable argument can be made that any observed effect will be unidirectional.
The authors summarize their case for why a marginal result such as the one observed in this study may be significant as follows:
In statistics, obtaining a probability value of P < .05 indicates that the obtained test statistic (based on one's sample) is extremely unlikely (less then 5% chance) to have been obtained by chance alone. By convention, this value is usually set at .05 (as a balance of type 1 and type 2 errors); however, this value is, in fact, arbitrary and statistical probability tables for hypothesis testing always include a range of probability values -- not only probability at the .05 level. Given that this is the first direct test of this hypothesis and considering the potential importance of finding a relation between mercury blood levels and autism, it is just as important to avoid a false negative as a false positive. As the original authors have now currently calculated, the obtained difference suggests that there is probably a real difference (specifically that the chance that a real effect exists is about 94%, or, conversely, that the chance the null effect is true is less than 6%, which misses the conventional .05 -- or 5% -- mark of statistical significance). Given the close value to conventional significance, most researchers would not call this a firm rejection of the hypothesis, but might say it was marginally significant. Most researchers facing a P value of .056 would not want to categorically state that results "indicate that there is no casual relation between mercury level . . . and autism." It concerns us that the original authors would want to let this conclusion stand in light of the new P value (which differs markedly from the .15 previously reported in 2004).
Another issue to consider is the question of a one-tailed or a two-tailed hypothesis test. Usually, researchers use a two-tailed test, which tests if there is a "difference" between 2 groups. However, when the literature leads a researcher to propose a specific direction of the difference, a one-tailed test is called for, "Often a researcher begins an experiment with a specific prediction about the treatment effect. For example, a special training program is expected to increase student performance, or alcohol consumption is expected to slow reaction times...The result is a directional test, or what is commonly called a one-tailed test."
Whether to use a one-tailed test or a two-tailed test can be decided based on considering what would happen if the results ended up in the opposite direction of what one suspects. In this case, it would mean that the blood mercury levels were lower in the autistic group. Would this support the original hypothesis? (No!) However, if this were to happen, that is, if the autistic group were significantly lower in their blood mercury levels than the normal group, the researchers would find themselves in the incongruous position of having to accept their hypothesis that autism is related to elevated levels of mercury in the blood! The key point here is that their hypothesis was directional, and a one-tailed test should have been used. In this case, the just missed significance of their new analysis using a two-tailed t-test (P = .056) would have reached a conventional level of statistical significance (with P < .03). (Emphasis mine. Citations removed.)
While I would like to avoid getting into an argument about whether a one-tailed or two-tailed t-test was appropriate in this particular case, I do take a bunch of conclusions from this paper.
First, I would like to make explicit that this study does not prove or disprove the link between autism and mercury. There is a great deal of evidence suggesting that mercury -- particularly the mercury used in vaccines -- is not causally related to autism. When making a scientific conclusion, you have to use a weight of the evidence approach. The fact that this study may have linked high mercury levels to kids with autism does not disprove those studies that found no effect, nor can a case-control study show causality.
On the other hand, it is always appropriate to recheck your data or the data of others. It is to the credit of scientists that we are willing to admit it when we had an answer wrong, and the process of science is predicated on this self-correction. There are some critics of the scientific process that point out that science makes errors of this nature relatively regularly. That is true; scientists are just as error-prone as everyone else. However, science remains the only organization that I know of that is as consistent in rectifying errors when they occur.
Fundamentally, that is why people trust us. Not because we are always right, but because when we are wrong we come clean.
Second, statistics are a tool for understanding reality, but if used improperly they can distort our understanding of reality. Recognizing that an effect is of marginal significance is important: it may be significant if you have more data. Just because something comes in at p-value =.056 doesn't mean that it doesn't matter. Just because something comes in at a p-value = .000001 doesn't mean that it is practically significant, even if it is statistically significant. When you interpret statistics -- either as a lay-person or as a scientist -- it is always good to remember that they provide access to reality, but they are not equivalent to reality.
Finally, the issue of mercury and autism is very controversial. Even though no causal link between mercury and autism has been found, this is clearly an issue about which people -- rightly or wrongly -- have very strong feelings. Issues of this nature are the times when it is most important to be careful with your data. You can't be cavalier about a study that concerns such a controversial issue because if you are then critics of science will just point to your attitude as evidence for the superfluity of your arguments.
We need to be very careful to cross our ts and dot our is in these cases because if we don't correct ourselves, someone else will. And it is never OK to hide parts of the evidence from the public. I like how the authors of this reanalysis concluded:
Of utmost importance (which outweighs the discomfort of writing about an error made by colleagues whom we know are generally competent researchers) is that potential researchers who are trying to understand what is and is not behind the rise in autism are not misled by even the slightest misinformation. It is imperative that researchers, medical professionals, and the public at large have the full set of information.
In science, we live or die by our honesty, and that sometimes includes admitting when we messed up.
Hat-tip: Faculty of 1000
UPDATE: More on this here.
- Log in to post comments
Using the two-tailed t-test was entirely appropriate, given that there was no good evidence to think that the result should go one way. Based on the real scientific evidence, mercury levels could have been higher or lower in autistic children. In fact, I'm of the mind that a one-tailed t-test is almost never appropriate. The only exception is if there's damned good evidence to think that the difference between groups, if it exists, would only go one way, and such cases are uncommon. This sums up why the Hitlan paper is dubious:
Exactly right. Moreover:
We also should consider a well-known informal rule that most new research students are likely exposed to in their statistics textbooks. One picks the type of tailed test, before one reviews the data. This is to prevent changing the type of test one uses to get a certain result. DeSoto & Hitlan by their own description had already reviewed the data and afterwards selected their one-tailed test. This violates the rule described above.
The Hitlan paper exists only to try to spin a positive result out of a negative result. The "investigators" probably saw a p value of around 0.11 in the original study and realized that if they used a one-tail t-test they could cut it in half, to near 0.05.
Oops. Bad blockquote tag on the last paragraph, which is from the blog post quoted.
In any case, I take issue with the claim that there was was an "error" calculating the p-value. The original paper got it right using the more conservative assumption (which was justified by a review of the literature). The Hitlan paper makes the less conservative assumption, even though the literature does not give clear guidance over whether we should expect higher or lower mercury levels in autistic children.
I don't disagree with you on matters of principle either that the one-tailed t-test is barely ever justified or that the it is better to make conservative assumptions. However, Hitlan do make a point that there were two outliers in the original Ip et al. study of greater than 3 SD. That is somewhat disconcerting and makes me wonder why they were outliers.
Furthermore, I was trying to argue that borderline results deserve rigorous analysis. I agree with you. I do not believe that the autism/mercury story is a real one, but in cases where it is close I think we need to be extra rigorous to prove our case.
That was my purpose in posting this article. Not necessarily because I agree with their findings or their argument, but because we are ethically responsible to be clear and honest about where our data is even slightly muddy.
Wouldn't this be a fantastic opportunity to apply effect sizes instead of p-values for interpreting the results?
I never said we weren't.
Unfortunately, this article isn't a particularly good example of applying "rigorous" analysis, and I'm not sure why two outliers would be such a concern. In any case, the authors clearly are biased (look at the some of the references, which cite Holmes and Blaxill, for cryin' out loud!) and were clearly looking for a way to make the data show something that it almost certainly does not support.
so i just read through all the blood mercury data and its errors, some just typographical. Also, i could not replicate Desoto and hitlan's calculations for their p values at all, it looked like they got it all wrong from the get go anyway. ok here goes my analysis. in the first paper, the average for the control group was reported to be 17.68. this was either a typo or a miscalculation as the average is really 14.68, which they corrected. the next error was the printing of the standard deviations, reported to be 2.48 and 5.65 for control and autistic group, respectively, when its supposed to be 12.49 and 15.65 (the number one was not printed in front for whatever reason)...this too was corrected to 12.48 and 15.65 (although 12.48 should be rounded to 12.49 as the value is 12.48795). their p value of 0.056 is different from their previous p value of 0.15. when i entered in the data, i received a p value of 0.0464, which is statistically significant (i used my own two-tailed t-test macro and an online t-test tool found here: http://www.quantitativeskills.com/sisa/statistics/t-test.htm but my macro only gave me the t-statistic which was equal to the online t-statistic). now either im entering numbers into the system incorrectly (not likely), or they made another typo in the erratum from 0.046 to 0.056 (likely). considering their previous sloppy work, id like to think this was another typo and my value is correct. also, i used a conservative effective degrees of freedom calculation.
Conclusion: i think it is important that you brought this to attention for the reason that you did, to show that data needs to be scrutinized. However, as you suggested, people should not give much credit to this. There is a wealth of data to show mercury is not associated with autism, especially of the thimerosal variety (just search eric fombonne, who even stated he feels guilty receiving so much grant support to show negative results over and over, that neither mercury or vaccines are the cause of autism). I truly hope people can move past this soon and not waste more time and effort.
Hi Jake,
I am one of the authors of blog rebuttal of DeSoto & Hitlan, that Orac linked to above.
I want to thank you for taking the time to discuss the DeSoto & Hitlan article. I strongly agree with you when you call for high standards and the integrity to make sure we admit and correct mistakes.
I am also grateful to Drs DeSoto & Hitlan for catching the statistical errors and for caring enough to inform the journal editor. I note that DeSoto & Hitlan wrote their critique at the request of the editor.
However.. DeSoto & Hitlan go way beyond just writing a new statistical analysis based on corrected numbers. They offer multiple new interpretations. It is in this aspect that myself, DoC, and others have a problem. After we wrote our rebuttal, Dr DeSoto herself decided to visit us. Her comments were quite interesting. You may wish to visit our post and review this yourself.
At the core of it, DeSoto & Hitlans argue that the issue is really important and that earlier studies indicate that there may be a relationship between mercury and autism; ergo even near statistical significance should be taken seriously.
DoC and I argue that the support for this premise is flimsy.
1) The authors argue that autism is a lot like mercury poisoning, they cite a non-peer reviewed journal article from Medical Hypotheses.
2) The DeSoto & Hitlan claim that an article in the European Journal of Pediatrics showed that autism has previously been diagnosed in an 11 month old boy until a later diagnosis of mercury poisoning was made. In reality the authors of that article write:
The diagnosis remained obscure. The child was referred for further evaluation of severe psychomotor regression with autistic features of unknown aetiology.
DoC and I would be interested to know if DeSoto & Hitlan plan on retracting or clarifying their take on this study, as their comments do not accurately reflect what those authors wrote.
3) DeSoto & Hitlan further state that autism in on the rise and propose that there could be an environmental cause for this. DoC criticized this in our post. Dr. DeSoto when she visited us took issue with this and wrote:
DoC has said that it is misleading at best to suggest that autism is on the rise. Give me a break. I am well aware that there is a controversy about how much of the increase in autism is due to more awareness and diagnostic issues. I am also well aware of the general consensus and the range of informed scientific opinion. Conservative estimates are that actual rise is three or four fold with the rest due to changes in diagnostic practices.
Unfortunately consensus papers on this subject are non-existent. Whats more both DoC myself fanatically follow the autism epidemiology. There are no papers that show a genuine 3-4 fold increase with the rest due to changes in diagnostic practice.
I dont mind that DeSoto & Hitlan have an opinion on this issue, but I do have a real problem with them confusing their opinion with scientific data.
Interverbal,
The more I think about it, the more I think you are dead-on. I printed a kind-of retraction here.
Saying that we need to admit all evidence and be critical of data is one thing, and I stand beside that statement. It doesn't sound like anyone is being critical of that.
However, I had no idea that they cited a non-peer reviewed paper in their critique. Further, if they are arguing that mercury poisoning and autism can be misdiagnosed, they need to provide reasonable evidence for that assertion. (Obviously the issue of autism epidemiology is a subject that you know more about than I do.)
De Soto and Hitlan can and do need to address those concerns, largely for the same reasons I think their criticisms should be published. Being critical is a double-edged sword, and now people need to think hard about whether their criticisms are reasonable.
It sounds like a lot of people are skeptical.